工程预测焊点疲劳寿命
- 2016-04-27 13:17:00
- Peter J.Heyes, Mikael 原创
- 8978
在汽车工业中,点焊被广泛地用于零部件和结构的制造。点焊构件的耐久性主要取决于焊点的疲劳强度。在一条生产自动线上装备一个焊点的点焊机械装置可能需要30万美元,为了补救某一问题而必须在生产时再增加一个点焊装置,其费用可能不止2倍。如果我们能在设计的早期预测焊点的疲劳寿命,那么显然这些费用可以降到最低点。更有意义的是,它也有助于缩短产品的开发周期,提高产品的质量。
Smith和Cooper用断裂力学方法研究过受剪切载荷焊点的疲劳寿命预测问题。他们指出:“一个焊点也许可以被认为是一个外表面有一环向深裂纹的实心圆棒,当这一圆棒受一个Ⅰ—Ⅱ复合型载荷时,它会在最大的局部Ⅰ型方向产生分叉裂纹并扩展”。他们说明了根据计算的裂纹扩展速率可以较好地预测焊点的疲劳寿命,并用他们的计算结果作出一些简单的设计曲线。Smith和Cooper所建议的方法基于对简单受剪搭接接头的有限元模拟,这种方法需要进一步的发展才能用于其它不同的焊点型式,处理变幅异相复杂载荷。发展的结果可能是一个简单的专门针对焊点的规范,按照英国标准BS7608的方法,给出适用于不同点焊类型的载荷—寿命曲线族。
事实上,关联不同加载条件下焊点的疲劳强度,载荷是一个相当糟糕的参量。Raji和Sheppard提到,不同型式受不同载荷的焊点,它的疲劳耐久性能够通过分析板内焊点周边的局部应力得到更好的理解,这一局部应力指的是焊点附近的结构应力。Rupp等人描述了如何计算这些结构应力。他们根据最大应力、最小应力和一个载荷谱对焊点的疲劳寿命进行了预测。本文介绍的技术类似于Rupp等人的工作,不同的是进一步地将结构应力计算与应力缩放、叠加以及应用瞬态有限元分析结果等方法结合起来。下面将先介绍软件的技术细节,然后给出两个说明简例。
1方法概述
方法要求将焊点模拟成为MSC/NASTRAN中的刚性梁单元;经这些梁单元传递的力和力矩被用来计算结构(名义)应力,这些应力为围绕焊点熔核和连接板的局部应力;按照S—N总寿命方法,用这些结构应力预估焊点的疲劳寿命。
软件系统由一些经过修改的MSC/FATIGUE模块组成,它的核心为焊点疲劳分析器SPOTW,图1表示了这一软件的框架。该系统当前只支持两板焊点的疲劳计算。焊点应当用连接两板中面且垂直于这两个中面的刚性梁表达,而板用位于板中面的壳单元模拟。焊点的长度因此是板厚之和的一半。焊点附近的网格不需要做任何细化,对壳单元的唯一要求是它们能将正确的力传至刚性梁。事实上,使用大尺寸的壳单元(大于2倍的熔核直径)似乎能获得最好的结果,即最实际的连接刚度。
软件的使用方式与标准的MSC/FATIGUE类似。通过填一组表格创造一个作业文件,这个文件包含了焊点的直径、板厚和疲劳性能参数信息。有一个解读器读这个文件,从MSC/PATRAN数据库中抽出所有的有关数据,写到一个中间文件中去。焊点分析器根据这个中间文件以及所需的载荷信号和疲劳性能数据,对每个焊点做寿命预测。最后输出2个计算结果文件,其中的一个文件为MSC/PATRAN的可读文件。下面将给出有关疲劳计算的一些细节。
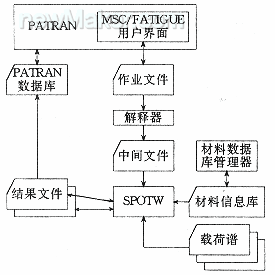
图1焊点疲劳分析系统框图
2.1结构应力计算
一个典型的焊点如图2所示。阴影部分为焊核,在有限元分析中,它被模拟成一个刚性梁单元,连接两块板的中面。梁单元的长度为0.5(s1+s2),其中s1和s2分别为板1和板2的厚度。点3位于焊核中心线两块板的接触位置,离点1的距离为0.5s1。所有的力和弯矩按图示的梁单元坐标系取。

图2典型焊点示意图
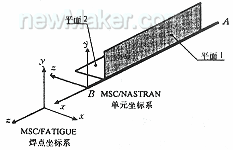
图3
对于点1,板中内表面的等效应力为熔核周向位置角的函数,可写成
σv1=-σmax(Fx1)cosθ-σmax(Fy1)sinθ+σ(Fz1)+σmax(Mx1)sinθ-σmax(My1)cosθ(1)
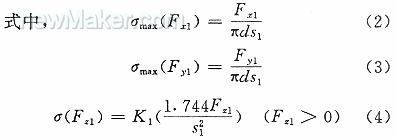
σ(Fz1)=0(Fz1≤0)(5)
即只有熔核轴向力中的拉伸分量对损伤有贡献
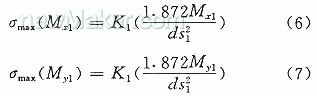
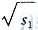 (这一常数作为对弯曲应力梯度影响的补偿);d为熔核直径。所有的长度单位为mm;力的单位为N;力矩单位为N*mm。
(这一常数作为对弯曲应力梯度影响的补偿);d为熔核直径。所有的长度单位为mm;力的单位为N;力矩单位为N*mm。 点2的结构应力计算方程和点1基本类似,不再重复。
熔核中的应力计算有点不同。Rupp等人建议每隔10°计算多个平面上的正向应力,即用基于应力的临界面方法,这意味着对于每个焊核需要进行648(36×18)次计算。显然,这种方法计算量非常大。考虑到焊点一般不会因裂纹扩穿熔核而引起失效,除非焊核直径与板厚相比很小,焊点的主要失效模式是裂纹穿透金属板。笔者使用了两种快速方法:一是忽略熔核失效的可能性;二是用MSC/FATIGUE中常用的绝对值最大主应力作为损伤参量,这种方法只需要做36次计算,其计算式为
τ=τmax(Fx3)sin2θ+τmax(Fy3)cos2θ(8)
σ=σ(Fz3)+σmax(Mx3)sinθ-σmax(My3)cosθ(9)
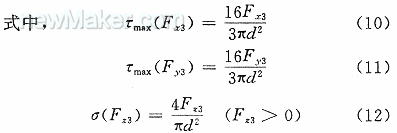
σ(Fz3)=0(Fz3≤0)(13)
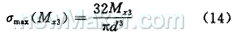
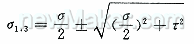 (15)
(15)
2.2材料性能
软件系统需要一组载荷比R=0条件下的S—N曲线,分别对应于焊核和金属板。另外也需要平均应力敏感度系数和标准差参量。这些S—N曲线为专门的焊点S—N曲线,与常规的母材材料S—N曲线截然不同。这些S—N曲线的数学式可表示为
ΔS=SRI1(Nf)b1(16)
式中,SRI1(应力范围截距)和b1(斜率)均为材料常数。上式适用于失效循环周数Nf小于过渡寿命Nc1的情况。如果Nf>Nc1,那么应该用第二斜率b2。对于每一个循环,平均应力可按下式修正,即计算R=0时的等效应力幅度
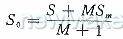 (17)
(17)
Rupp等人描述了对应于钢板和焊核的通用S—N曲线,数据有一个相当宽的分散带,部分反映了这些数据代表了多种钢板中的焊点,既有中强钢也有高强钢。如果只对某一特定材料,分散带可能会窄一些。
2.3损伤计算
损伤计算在两块板和焊核中沿着焊点的周向以10°的间隔进行,因此,对于每个焊点,共108个疲劳计算。通过静态放大叠加一组静态载荷结果,或通过瞬态有限元分析计算力和力矩;使用上面介绍的公式从力和力矩中计算每个计算点的有效应力变化;然后用雨流循环计数技术获得范围—均值直方图;最后根据直方图及Miner损伤累积规则计算疲劳损伤。结果输出为两个文件:一个是MSC/PATRAN 2.5 .els文件,用MSC/PATRAN可以对它进行后处理;另一个为ASCII文件,它包含了更为详细的结果,可用SPOTW进行后处理。
本文描述的方法计算量较大,计算时间基本上和载荷谱中的数据点数目成比例,因此,有效地过滤载荷输入能够节省大量计算时间。
3计算简例
3.1实验室用试件
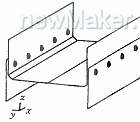
图4H型实验室点焊试件
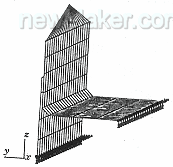
图5H型试件有限元模型
这些试件的载荷—寿命曲线用上面介绍的分析软件进行预测。计算所用的焊点S—N曲线为ST1403材料的焊点曲线,其板厚介于0.66~2.5 mm之间,焊点熔核的直径变化范围为3.5~6.5 mm。图6比较了试验和计算结果,计算结果对应于3个不同的成活率。
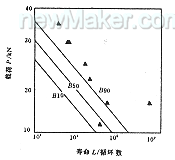
图6计算结果与试验结果比较
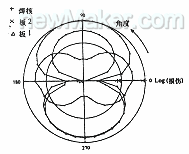
图7焊点极坐标损伤图
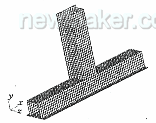
图8T型梁试件的有限元模型
它由厚度为1和0.8 mm的薄板组成。该梁的有限元网格如图8所示,梁的两端固定,在垂直端受x和z方向的载荷。表1列出了3种加载情况下的试验结果和分析结果。分析中我们同样使用LBF给出的焊点通用S—N曲线。
上面的分析比较表明,试验结果与分析结果的关联似乎是合理的,分析结果比试验结果要保守一些。
表1T型梁试件的预测寿命和试验结果比较
载荷(N) 试验寿命(循环周数) 预测寿命(循环周数)
F(x)变幅=157.5 R=0.1 460 000 536 300
F(z)变幅=503 R=-1 70 000 35 024
F(z)变幅=400 R=-1 290 000 134 500
4结语
本文描述的焊点疲劳寿命预估软件系统主要基于德国LBF实验室Rupp等人的工作,是德国LBF疲劳实验室、英国nCode和美国MacNeal-Schwendler公司的一个合作成果。通过有限元静态载荷分析或者瞬态分析,结合应力简化计算,它能计算实际载荷工况下的焊点疲劳损伤。软件具有良好的用户界面,它能方便地帮助分析人员判断寿命最短的焊点位置。当前这一系统已经用于汽车底盘、悬架系统以及车体的耐久分析。但是这一技术还需要进一步的、广泛的试验验证。
(end)
相关文章
- [焊接技术] 铝螺柱焊接对焊接夹具的设计要求 2024-12-28
- [焊接技术] 螺柱焊机发展史及其焊接工艺 2022-07-11
- [焊接技术] 干了多年的焊工都未必真能说清楚CO2、MIG/MAG和脉冲MIG/MAG的区别! 2020-12-23
- [焊接技术] 铝合金焊接中最关键基础知识,一定要知道! 2020-11-12
- [焊接技术] 铝合金氩弧焊缺陷及防止措施,果断收藏! 2020-11-07
- [焊接技术] 铝及铝合金焊接工艺详解! 2020-11-07
发表评论
社区新帖
- GBT 19867.4-2008 激光焊接工艺规程.pdf 2019-12-25
- GBT 2652-2008 焊缝及熔敷金属拉伸试验方法.pdf 2019-12-25
- GBT 16672-1996 焊缝-工作位置-倾角和转角的定义.pdf 2019-12-25
- GBT 16745-1997 金属覆盖层产品钎焊性的标准试验方法.pdf 2019-12-25
- GBT 17853-1999 不锈钢药芯焊丝.pdf 2019-12-25
- GBT 15169-1994 钢熔化焊手焊工资格考核方法.pdf 2019-12-25
- GBT 15579.5-2005 弧焊设备安全要求 第5部分 送丝装置.pdf 2019-12-25
- GBT 15579.7-2005 弧焊设备安全要求第7部分:焊炬(枪).pdf 2019-12-23
联系我们
| 联系人: | 韩玉琦 |
|---|---|
| 电话: | 0755-26013200/26013464 |
| 传真: | 0755-26013188 |
| Email: | saw@sawchina.cn |
| QQ: | 2280915288 |
| 微信: | 18682260315 |
| 旺旺: | szhbkj |
| 地址: | 东莞市凤岗镇东深路凤岗段206号天安深创谷W2栋诚信大厦21楼 |










































